Project summary and goals
The Earthshine Visibility Project is an ongoing effort to characterize the ability of the human visual system to detect very small differences in illumination between lit targets in a setting outside the controlled environment of a laboratory. The aim of the Project is to measure the threshold detection contrast of the unaided eye for a variety of observers (different ages, different locations, etc.) to characterize the range of possible values describing the population at large. The result will be a calibration curve that can be applied to other situations where we don’t necessarily know what the detection threshold is.
Background
The Project stems from my related work on the so-called “Ashen Light” of Venus, a phenomenon known to astronomy for almost 400 years but still lacking a widely accepted explanation. For more information on the Ashen Light, see these links:
In 2021, Springer published my book "Mystery of the Ashen Light of Venus: Investigating a 400-Year-Old Phenomenon". The contents in part touch on the analogy between the Ashen Light and the phenomenon of Earthshine. This is a familiar sight around the time of the new Moon, when the Moon is a crescent. Light from the Sun reflects off the Earth toward the Moon. The light reflects again off the Moon, and heads back toward the Earth. Since some of the reflected light comes from the portion of the Moon’s disk that is not directly illuminated by the Sun, the Earthshine gives the impression of very faint light lighting up the otherwise unseen part of the Moon’s disc. In folklore, Earthshine is sometimes referred to as the “old moon in the new moon’s arms”.
- The four-hundred-year mystery of the Ashen Light of Venus (io9, 2013)
- The Mystery of Venus’ Ashen Light (Universe Today, 2012)
- The enigmatic ashen light of Venus: an overview (Journal of the British Astronomical Association, 2000)
In 2021, Springer published my book "Mystery of the Ashen Light of Venus: Investigating a 400-Year-Old Phenomenon". The contents in part touch on the analogy between the Ashen Light and the phenomenon of Earthshine. This is a familiar sight around the time of the new Moon, when the Moon is a crescent. Light from the Sun reflects off the Earth toward the Moon. The light reflects again off the Moon, and heads back toward the Earth. Since some of the reflected light comes from the portion of the Moon’s disk that is not directly illuminated by the Sun, the Earthshine gives the impression of very faint light lighting up the otherwise unseen part of the Moon’s disc. In folklore, Earthshine is sometimes referred to as the “old moon in the new moon’s arms”.
Earthshine on the night side of a four-day-old crescent moon, 15 March 2013. Photographed by Adam Evans / CC BY-NC 2.0.
Earthshine results from a process we know can’t explain the Ashen Light of Venus, but the circumstances are otherwise superficially similar in terms of the observation: a faint light illuminates the part of the Moon not directly illuminated by the Sun. It’s vastly fainter than the bright light seen toward the crescent. It’s easily detectable by the eye alone against a dark sky, but it’s invisible during the daytime because the brightness of the daytime sky overwhelms it. That means there’s a threshold point at which the Earthshine sufficiently exceeds the surface brightness of the (twilight) sky around it that the eye and brain see a positive contrast and detect the light. We’re interested in knowing what that contrast value is, because it tells us something about the sensitivity of the eye and brain system.
Surprisingly, there doesn’t seem to be any published research about this. Most vision studies, going back to the 1940’s, use controlled laboratory settings to measure human responses to faint light. Earthshine seen against twilight sky luminances of different values could be a fairly sensitive test of detection contrast threshold useful for predicting detection probabilities for the Ashen Light and other faint light phenomena.
At the end of the study, we hope to understand better the sensitivity of the unaided human eye to very small increments of threshold contrast. The sensitivity calibration will be applied to historical accounts of observations of the Ashen Light of Venus in order to help discriminate among several hypotheses that account for its appearance, whether real (i.e., part of the atmosphere of Venus) or false (i.e., a trick of the optics in telescopes).
The bottom-line goal is to use the calibration to figure out how bright the Ashen Light would have to be to possibly trigger a visual detection by observers on Earth using small telescopes, in order to explain the historical record of such observations. If we knew what that luminance was for the AL, we could work backward to figure out what the light emission at the top of the Venus atmosphere is. With that number in hand we would have a better basis for comparing it against various physical mechanisms on Venus that might explain the AL (or rule it out entirely).
Surprisingly, there doesn’t seem to be any published research about this. Most vision studies, going back to the 1940’s, use controlled laboratory settings to measure human responses to faint light. Earthshine seen against twilight sky luminances of different values could be a fairly sensitive test of detection contrast threshold useful for predicting detection probabilities for the Ashen Light and other faint light phenomena.
At the end of the study, we hope to understand better the sensitivity of the unaided human eye to very small increments of threshold contrast. The sensitivity calibration will be applied to historical accounts of observations of the Ashen Light of Venus in order to help discriminate among several hypotheses that account for its appearance, whether real (i.e., part of the atmosphere of Venus) or false (i.e., a trick of the optics in telescopes).
The bottom-line goal is to use the calibration to figure out how bright the Ashen Light would have to be to possibly trigger a visual detection by observers on Earth using small telescopes, in order to explain the historical record of such observations. If we knew what that luminance was for the AL, we could work backward to figure out what the light emission at the top of the Venus atmosphere is. With that number in hand we would have a better basis for comparing it against various physical mechanisms on Venus that might explain the AL (or rule it out entirely).
A false start
I began collecting data for this project in 2016 by making my own visual estimates of two times each night during the week after new moon:
The first time would naturally precede the second given that the brightness of the sky surrounding the Moon was constantly decreasing a the Sun's altitude with respect to the horizon became progressively more negative after sunset. The difference in brightness of the adjacent sky between the two detections would then be a sort of first-order guess as to the detection probability in cases where the circumstances were very close to those in famous lab experiments that attempted to measure "threshold contrasts" among visual observers. But how bright were the Earthshine and sky light at those two instants?
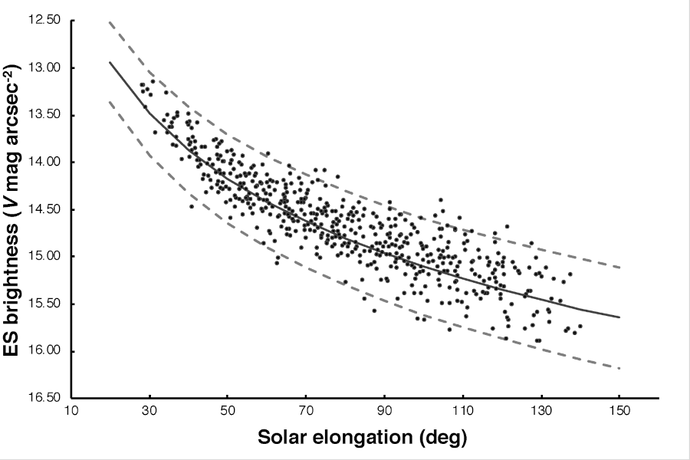
I had no way of measuring either at the time, so instead I modeled them. For the Earthshine brightness I fit a function to the observations of Montañés-Rodríguez, Pallé and Goode (2007). This plot shows the data with a power-law fit (solid line) with a constant of 31.8 ± 1.26 and an index of −1.23 ± 0.03, and 95% confidence intervals (dashed lines).
- The time of a "liminal" detection (when I first sensed the possibility that the night side of the Moon could be seen against the twilight sky)
- The time of a "confident" detection (when there was no doubt in my mind that the Earthshine was visible).
The first time would naturally precede the second given that the brightness of the sky surrounding the Moon was constantly decreasing a the Sun's altitude with respect to the horizon became progressively more negative after sunset. The difference in brightness of the adjacent sky between the two detections would then be a sort of first-order guess as to the detection probability in cases where the circumstances were very close to those in famous lab experiments that attempted to measure "threshold contrasts" among visual observers. But how bright were the Earthshine and sky light at those two instants?
I had no way of measuring either at the time, so instead I modeled them. For the Earthshine brightness I fit a function to the observations of Montañés-Rodríguez, Pallé and Goode (2007). This plot shows the data with a power-law fit (solid line) with a constant of 31.8 ± 1.26 and an index of −1.23 ± 0.03, and 95% confidence intervals (dashed lines).
So, to within the uncertainties on the fit parameters, we have a simple relationship that predicts the surface brightness of the Earthshine on the night side of the Moon as a function of the elongation angle of the Moon with respect to the Sun at the time of observation. That angle changes rather slowly in comparison to the rate at which the brightness of the sky changes during twilight, so it's fair to assume that the Earthshine brightness really doesn't change during the typical time interval I found from liminal to confident detections.
But I ran into trouble with computing the brightness of the twilight sky from a model. It turns out to be a surprisingly complex thing to calculate, and different models gave surprisingly large differences in the brightness of the sky in a particular direction at a particular moment in time. The model I landed on seemed to consistently overpredict the sky brightness. I realized I needed to take a different approach, namely to measure it directly and dispense with the model uncertainties.
The other difficulty involved obtaining the visual timings of the Earthshine's appearance in twilight. I could have simply made all the observations myself. My (corrected) visual acuity is decent and I have extensive experience with visual observations of the night sky. But I also knew that there were sometimes considerable variations among observers presented with the same visual stimulus, and I thought I might try to crowdsource observations from many individuals that would then account for this variation. In around 2017-2020 I did exactly that, and a number of people offered to help by making observations.
But in the end, with an unreliable model of the twilight sky brightness and differences among observers that were larger than I expected (presumably due to varying observing experience), I abandoned the idea of using crowdsourced data and reverted to myself as the single observer. (That said, I still want to do an experiment where I gather dozens or hundreds of people in one place to make timings under identical conditions and find out just how wide the distribution of times is.)
In short, all this led to me jumping the gun and submitting a manuscript to an astronomy journal that really wasn't ready for primetime. It's the only instance where I withdrew a paper that I submitted after a referee rightly pointed out a lot of problems with it. It wounded my pride somewhat, but it was an important opportunity for learning and growth. So I went back to the drawing board and rethought the experiment in 2021.
But I ran into trouble with computing the brightness of the twilight sky from a model. It turns out to be a surprisingly complex thing to calculate, and different models gave surprisingly large differences in the brightness of the sky in a particular direction at a particular moment in time. The model I landed on seemed to consistently overpredict the sky brightness. I realized I needed to take a different approach, namely to measure it directly and dispense with the model uncertainties.
The other difficulty involved obtaining the visual timings of the Earthshine's appearance in twilight. I could have simply made all the observations myself. My (corrected) visual acuity is decent and I have extensive experience with visual observations of the night sky. But I also knew that there were sometimes considerable variations among observers presented with the same visual stimulus, and I thought I might try to crowdsource observations from many individuals that would then account for this variation. In around 2017-2020 I did exactly that, and a number of people offered to help by making observations.
But in the end, with an unreliable model of the twilight sky brightness and differences among observers that were larger than I expected (presumably due to varying observing experience), I abandoned the idea of using crowdsourced data and reverted to myself as the single observer. (That said, I still want to do an experiment where I gather dozens or hundreds of people in one place to make timings under identical conditions and find out just how wide the distribution of times is.)
In short, all this led to me jumping the gun and submitting a manuscript to an astronomy journal that really wasn't ready for primetime. It's the only instance where I withdrew a paper that I submitted after a referee rightly pointed out a lot of problems with it. It wounded my pride somewhat, but it was an important opportunity for learning and growth. So I went back to the drawing board and rethought the experiment in 2021.
Take two...
In the intervening time I obtained (secondhand) a calibrated luminance meter. This is an electronic device that measures the surface brightness of a scene within a specified field of view; in the case of my meter, it is a 1º circle. Whenever I made Earthshine visibility timings, I started also measuring the brightness of the twilight sky adjacent to the lunar disc. By centering the field of view a half degree north and east of the Moon's center, doing so ensured that the field would not include any light from the Earthshine itself. Rather, it would be essentially tangent to the lunar disc at the point opposite the direction toward the Sun. The result, which is averaged over the field, is a pretty good representation of how bright the sky is against which is seen the night side of the Moon.
As of the end of 2023 I made measurements on about 60 individual dates. The reason that there are so relatively few is that in order for an observation to be valid there must be no clouds, dust or mist anywhere in the direction of the Moon on the sky. Otherwise, these influences could change the contrast between the lunar disc and the twilight sky. So I only make timings under substantially clear conditions, noting any suggestion of clouds anywhere else in the sky. I also record basic meteorological data like the ambient temperature and relative humidity, which can change the optical transparency of the air.
Based on those few dozen observations, some insights are emerging.
As of the end of 2023 I made measurements on about 60 individual dates. The reason that there are so relatively few is that in order for an observation to be valid there must be no clouds, dust or mist anywhere in the direction of the Moon on the sky. Otherwise, these influences could change the contrast between the lunar disc and the twilight sky. So I only make timings under substantially clear conditions, noting any suggestion of clouds anywhere else in the sky. I also record basic meteorological data like the ambient temperature and relative humidity, which can change the optical transparency of the air.
Based on those few dozen observations, some insights are emerging.
Comparison with a visibility model
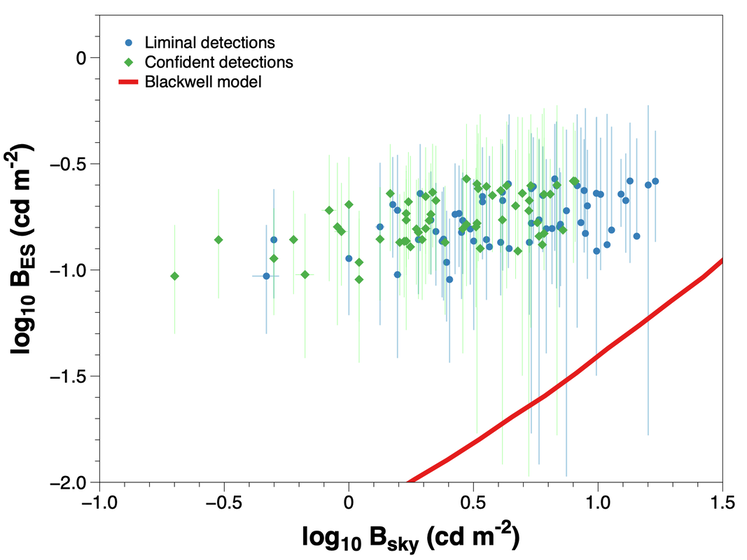
First, I plotted my observations as target vs. background luminance. To compress a large dynamic range into a reasonably sized plotting area, in vision research these are usually rendered in log-log space. On the same plot, I added an empirical model from H. Richard Blackwell's classic 1946 paper "Contrast Thresholds of the Human Eye". The model is the result of millions of individual observations made by human subjects in laboratory conditions and indicates the relationship between the variables that is statistically likely to provoke a positive detection.
Here, "B_ES" means the modeled surface brightness of the Earthshine and B_sky means the measured surface brightness of the adjacent twilight sky. My data don't quite follow Blackwell's curve; rather, the points cluster at lower sky brightnesses than the model predicts. The first challenge of the project now is to try to understand why this is. It's possible that my luminance meter just reads consistently low. But the other unexpected element of this plot is that there's not a lot of variation in the corresponding Earthshine brightness at the moment of visual detection across a relatively large range of sky brightnesses. In other words, the cloud of points doesn't fall along a curve; rather, it's pretty flat. I suspect something is going on beyond just the meter, but I don't yet know what.
Threshold contrast vs sky brightness
We can also look at how the contrast between target (Earthshine-lit Moon) and background (adjacent twilight sky) varies according to the sky brightness. For an opaque object seen in front of a background, contrast is defined as the ratio of the difference in brightness between the object and background to the brightness of the background (C = ΔB / B, where ΔB = B_object - B_background). This relation holds over many log decades of background brightness. But when an object is viewed through something like a transparent screen — much like looking at an astronomical object through the atmosphere whose luminance is greater than zero due to scattered sunlight — the "foreground" in the direction of the object contributes the same luminance as the "background", so B_background = B_object. The contrast therefore reduces to C = B_object / B_background. In the case of the Earthshine, this is C = B_Earthshine / B_sky.