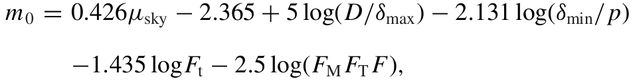What is the probability of seeing any particular astronomical object through a telescope?
In recent years, the overlap of two adjacent interests — light pollution research and visual observations of objects through telescopes — led me to ask a question: what influences the chances that an observer will see any particular object under a given set of observing circumstances? In particular, this question stemmed from another question I asked while I was writing a book about the so-called "Ashen Light" of Venus: what is the smallest quantity of light that the human eye can reliably sense? In talking to vision science researchers and reading some of the papers in their field, I became convinced that the human eye is a highly underrated detector of faint light.
One of those researchers is Dr. Andrew Crumey, a professor at Northumbria University in Newcastle, U.K. Both a theoretical physicist and a published novelist, he occupies an unusual position in academia. I first learned of his work on these questions when I read his 2014 paper in Monthly Notices of the Royal Astronomical Society titled "Human contrast threshold and astronomical visibility". It's a paper I have come back to again and again in the roughly decade since it was published. In it, Dr. Crumey begins with foundational laboratory studies on human vision going back to the 1940s and derives formulae describing the expected visibility of different kinds of objects to the eye both with and without telescopic aid.
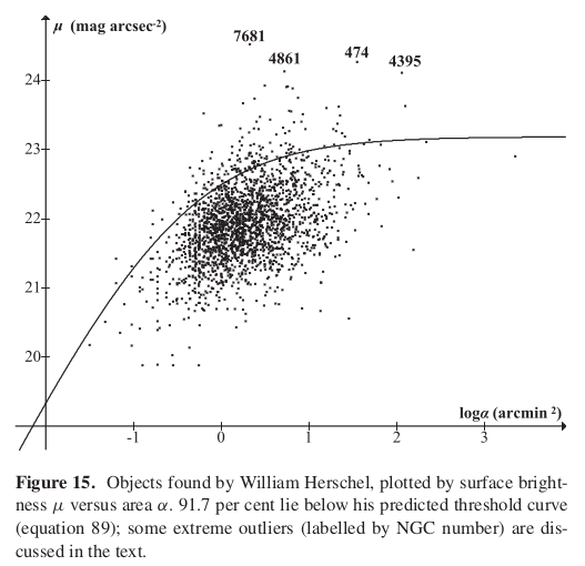
In particular, his Figure 15 got my attention:
One of those researchers is Dr. Andrew Crumey, a professor at Northumbria University in Newcastle, U.K. Both a theoretical physicist and a published novelist, he occupies an unusual position in academia. I first learned of his work on these questions when I read his 2014 paper in Monthly Notices of the Royal Astronomical Society titled "Human contrast threshold and astronomical visibility". It's a paper I have come back to again and again in the roughly decade since it was published. In it, Dr. Crumey begins with foundational laboratory studies on human vision going back to the 1940s and derives formulae describing the expected visibility of different kinds of objects to the eye both with and without telescopic aid.
In particular, his Figure 15 got my attention:
One of the outputs of Crumey's work is a model that predicts the likelihood of an individual telescopic observer seeing objects of a given surface brightness as a function of apparent angular size. To demonstrate use of the model, he applied it to the prolific observations of the Anglo-German astronomer William Herschel (1738-1822). Over nearly a half-century, Herschel observed thousands of objects in the heavens using what for their time were very large telescopes. Many of the objects Herschel saw were previously known. With the help of his sister, Caroline Herschel (1750-1848), he kept meticulous notes on what he saw. That allowed Crumey to compare his model against an extensive and largely consistent set of observations made by an individual observer.
The cloud of dots in the figure represents Herschel's objects in a space defined by two variables: the surface brightness of each object versus the angular area each subtends. The surface brightness is expressed in units of magnitudes per square arcsecond, an astronomer unit that follows a base-2.5 logarithmic trend with increasing brightness. The angular extent is given in a unit called a square arcminute. As a point of reference, the Moon as seen from Earth has an area of about 758 square arcminutes.
The solid line in the figure is Crumey's model specific to William Herschel, given factors like the size of the telescope he used, the (measured) diameter of the pupils of his (dark-adapted) eyes, and the presumed brightness of the night sky in Herschel's era. The model says that the chances of the observer it represents sees a particular object are better below the curve than above it. And sure enough, the data points tend to mostly fall below the curve.
I wondered whether I could run through the calculations and compute a model for my own local situation. I have observed from my current site regularly since 2020. In that time, little has changed here: I use the same telescope (20-cm, f/3.8 Newtonian) to make visual observations of various objects, and the brightness of the night sky is about the same now as it was three years ago. My observing logs say whether or not I found particular objects, so I could compare that to Crumey's model for my circumstances as Crumey did for William Herschel.
For this, I used a transcription of objects from Burnham's Celestial Handbook made by Steve Coe of the Saguaro Astronomy Club (SAC). A couple of years ago I ingested this into a Google Sheet and arranged the contents into cells for use in constructing observing lists. Burnham's is a classic of astronomical literature, compiled by Robert Burnham, Jr., of the Lowell Observatory over countless cloudy nights in the 1960s and 1970s. The Handbook lists just short of 2,000 objects around the night sky, of which about 2/3 are in principle observable from my latitude. Many are drawn from the New General Catalog of Nebulae and Star Clusters, or NGC. These tend toward brighter objects that many amateur astronomers can see with modestly sized telescopes.
I pulled from my master list a subset of those objects I attempted to observe since 2020 and put them into a new sheet. I sorted the observations into two tabs, "Seen" and "Not Seen" (which includes some marginal detections). I ditched most of the information in the table except for certain fields:
The cloud of dots in the figure represents Herschel's objects in a space defined by two variables: the surface brightness of each object versus the angular area each subtends. The surface brightness is expressed in units of magnitudes per square arcsecond, an astronomer unit that follows a base-2.5 logarithmic trend with increasing brightness. The angular extent is given in a unit called a square arcminute. As a point of reference, the Moon as seen from Earth has an area of about 758 square arcminutes.
The solid line in the figure is Crumey's model specific to William Herschel, given factors like the size of the telescope he used, the (measured) diameter of the pupils of his (dark-adapted) eyes, and the presumed brightness of the night sky in Herschel's era. The model says that the chances of the observer it represents sees a particular object are better below the curve than above it. And sure enough, the data points tend to mostly fall below the curve.
I wondered whether I could run through the calculations and compute a model for my own local situation. I have observed from my current site regularly since 2020. In that time, little has changed here: I use the same telescope (20-cm, f/3.8 Newtonian) to make visual observations of various objects, and the brightness of the night sky is about the same now as it was three years ago. My observing logs say whether or not I found particular objects, so I could compare that to Crumey's model for my circumstances as Crumey did for William Herschel.
For this, I used a transcription of objects from Burnham's Celestial Handbook made by Steve Coe of the Saguaro Astronomy Club (SAC). A couple of years ago I ingested this into a Google Sheet and arranged the contents into cells for use in constructing observing lists. Burnham's is a classic of astronomical literature, compiled by Robert Burnham, Jr., of the Lowell Observatory over countless cloudy nights in the 1960s and 1970s. The Handbook lists just short of 2,000 objects around the night sky, of which about 2/3 are in principle observable from my latitude. Many are drawn from the New General Catalog of Nebulae and Star Clusters, or NGC. These tend toward brighter objects that many amateur astronomers can see with modestly sized telescopes.
I pulled from my master list a subset of those objects I attempted to observe since 2020 and put them into a new sheet. I sorted the observations into two tabs, "Seen" and "Not Seen" (which includes some marginal detections). I ditched most of the information in the table except for certain fields:
Column header |
Information content |
MAG |
Integrated magnitude |
SUBR |
Surface brightness (magnitudes per square arcsecond) |
SIZE_MAX |
The large dimension of the object. A lower case "m" was used for arcminutes and a lower case "s" was used for arcseconds. In general, only Planetary Nebulae have sizes in arcseconds. A lower case "d" is used for degrees. |
SIZE_MIN |
The small dimension of the object. A lower case "m" was used for arcminutes and a lower case "s" was used for arcseconds. |
I converted all the numbers in SIZE_MAX and SIZE_MIN to arcminutes and dropped the letters. To get a number for Crumey's variable "ɑ" (the angular size of the object in square arcminutes), I approximated it by multiplying SIZE_MAX by SIZE_MIN and outputting the result into a new column, ALPHA. I stripped out some objects seen only visually (without telescopic aid), like the LMC and the Coal Sack. I also deleted entries for which SUBR=99.9 (i.e., no measurement).
The surface brightness estimates in the SAC compilation of the Burnham's list didn't seem right, so I estimated them from scratch today assuming that (1) the reported integrated magnitudes are correct, and (2) the angular extents are correct. I recomputed the angular surfaces according to:
To get the surface brightnesses in magnitudes per square arcsecond, I used this procedure:
1. Convert the integrated magnitude to flux
2. Convert the angular surfaces from square arcminutes to square arcseconds
3. Run the magnitude formula the other way
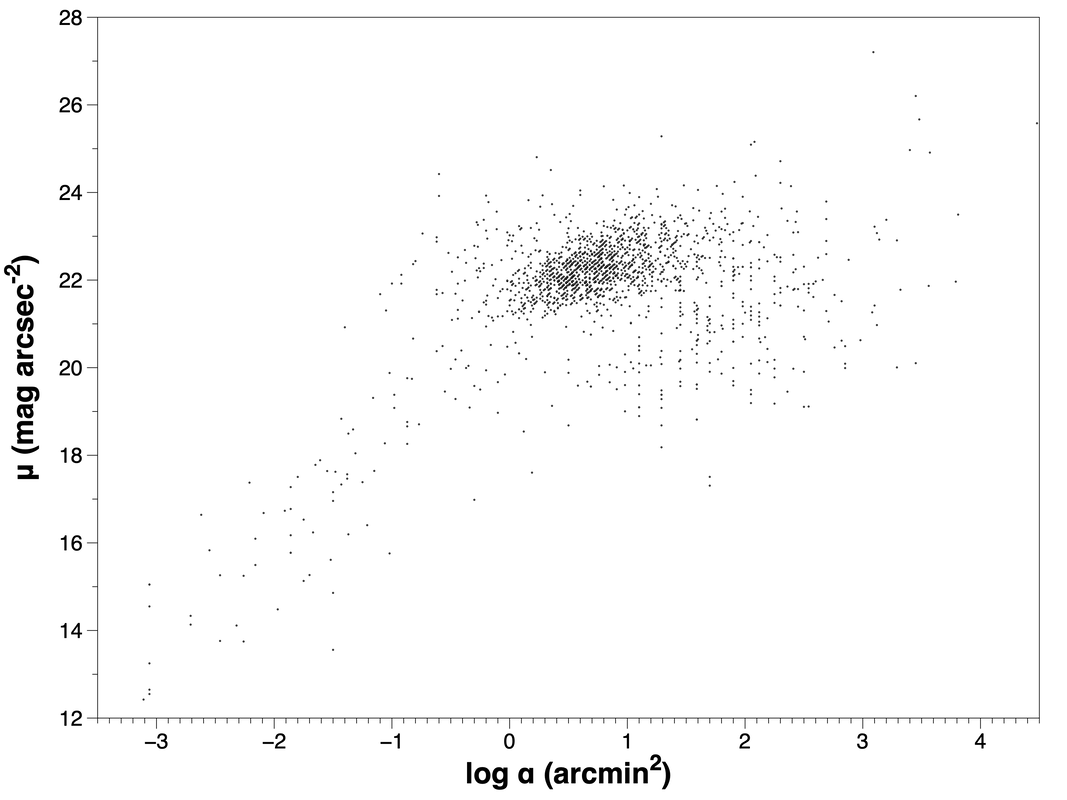
That gives numbers that make a lot more sense. For, e.g., M33 I get an average surface brightness of about 23 magnitudes per square arcsecond, which is close to the right number. The result is pretty much as I expected:
The surface brightness estimates in the SAC compilation of the Burnham's list didn't seem right, so I estimated them from scratch today assuming that (1) the reported integrated magnitudes are correct, and (2) the angular extents are correct. I recomputed the angular surfaces according to:
- If two dimensions were given, assume a rectangle with those dimensions; or
- If only one dimension was given, assume it was a diameter and use that to calculate the area of a circle with that diameter
To get the surface brightnesses in magnitudes per square arcsecond, I used this procedure:
1. Convert the integrated magnitude to flux
2. Convert the angular surfaces from square arcminutes to square arcseconds
3. Run the magnitude formula the other way
That gives numbers that make a lot more sense. For, e.g., M33 I get an average surface brightness of about 23 magnitudes per square arcsecond, which is close to the right number. The result is pretty much as I expected:
There again, like in the Herschel plot, is a cloud of points corresponding to objects that are a few square arcminutes in angular extent and have M33-like surface brightnesses. These are galaxies at mostly intermediate distances from Earth. In the lower left corner, corresponding to bright/tiny things, the points tend to represent planetary nebulae in our own Milky Way. Toward the upper right, the big/faint things are objects like relatively nearby dwarf galaxies, very loose/extended open clusters, and old supernova remnants.
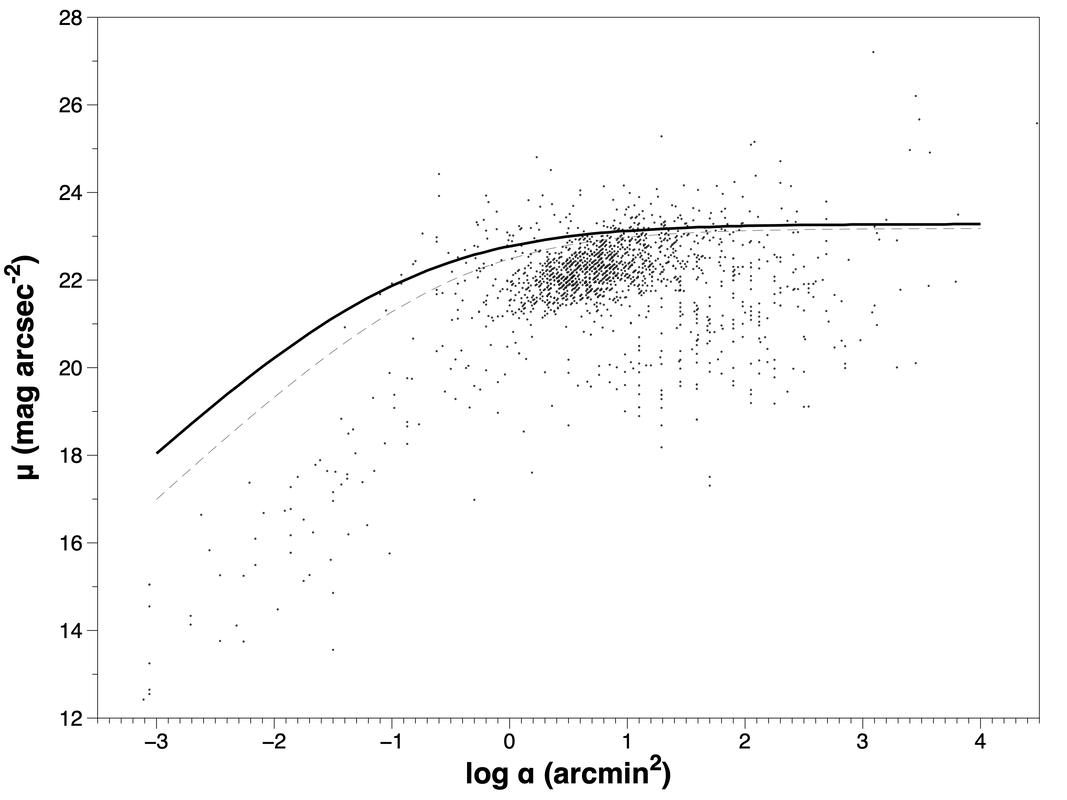
I computed a personal model from Crumey's formulae, estimating the parameters as best I could. Then I overplotted that model on the figure above as a solid black line. For kicks, I added in the Herschel model that Crumey published in his paper as a dashed black line.
I computed a personal model from Crumey's formulae, estimating the parameters as best I could. Then I overplotted that model on the figure above as a solid black line. For kicks, I added in the Herschel model that Crumey published in his paper as a dashed black line.
In both cases, the non-zero brightness of the night sky itself sets a "floor" beyond which observability of faint, extended objects is mostly impossible. That is why the curve beginning at left doesn't continue to increase with log ɑ. The separation between the lines results from the fact that Herschel and I observed under different circumstances: he had a telescope with a larger aperture and his observing site was essentially devoid of light pollution.
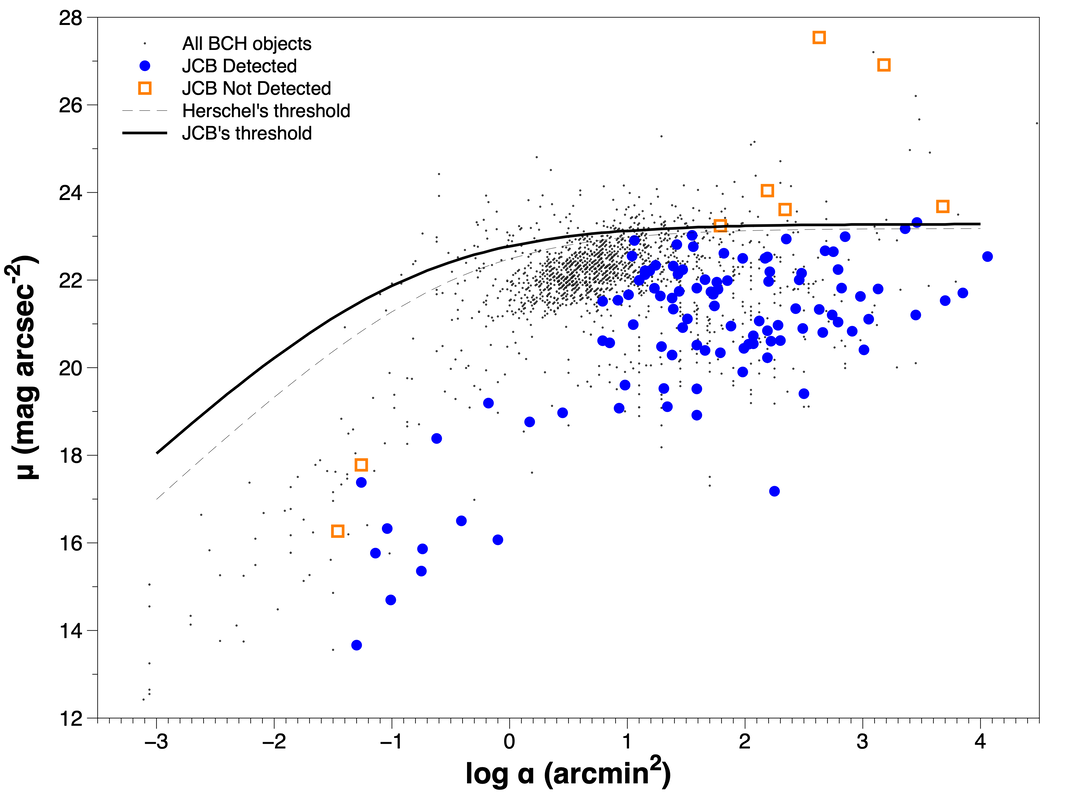
So how well does the model compare to my actual observations? In the next plot, I add in the objects I have attempted from my site. In the plot below, the filled blue circles are objects that I saw and the open orange squares are those I attempted but did not see.
So how well does the model compare to my actual observations? In the next plot, I add in the objects I have attempted from my site. In the plot below, the filled blue circles are objects that I saw and the open orange squares are those I attempted but did not see.
For the most part, the Crumey model seems to be pretty accurate. Nearly all the blue dots fall below the solid black line, while most of the red squares lie above it. The two red squares at lower left are kind of a mystery; both are planetary nebulae (IC 4593 and IC 4634). I'm certain that I did not see either object. Both have high surface brightnesses but they're really small, only a few arcseconds across. It remains a mystery for now. To further develop this test, I would like to deliberately target more objects close to the predicted threshold of visual detection for me and try to better determine exactly where the cutoff is.
Already this test has yielded some useful conclusions about which objects I should try to observe (exactly because I am like to see them) versus those that I can confidently write off for expected lack of observability.
Already this test has yielded some useful conclusions about which objects I should try to observe (exactly because I am like to see them) versus those that I can confidently write off for expected lack of observability.
How bright is the faintest star I can see with my telescope?
I'm also interested in reproducing Crumey's model for telescopic point-source detection. He goes back to Blackwell (1946) and Knoll (1946) to derive a formula based on the notion of a "just-perceptible difference". This gets at the smallest difference in levels of a perceptual stimulus that a person can detect with confidence. In particular, it is a consequence of Weber's Law, which holds that the minimum increase of stimulus which will produce a perceptible increase of sensation is proportional to the pre-existent stimulus. Over a fairly large range of input brightness, human vision tends to follow Weber's Law.
From this Crumey finds a "very good approximation" to the limiting magnitude of stars seen through a telescope (his Equation 69):
From this Crumey finds a "very good approximation" to the limiting magnitude of stars seen through a telescope (his Equation 69):
Without going too deeply into the details, this tells the brightness (magnitude) of the faintest star a particular observer can see through a telescope with an aperture D under a night sky of brightness μ_sky, given the diameter of the telescope exit pupil (d) and eye pupil (p), the inverse of the telescope's throughput (F_t) and a series of "field factors" that are either dependent or independent of the magnification the telescope and eyepiece combination.
This formula suggests how the limiting magnitude would change with night sky brightness assuming all other variables are fixed, which is true for a given setup. All of my observations were made with a telescope for which D = 200 mm. The exit pupil is calculated as the the focal length of the eyepiece in millimeters divided by the focal ratio of the telescope (in my case, f/3.8). I typically observe with a 12.5 mm orthoscopic eyepiece that gives a magnification of 61× and a field of view of just about 0.5º. That means the exit pupil is about 3.3 mm. A lab measurement of the diameter of the dark-adapted pupil for people about my age is 6.15 mm (Bradley et al. 2011). However, the brightness of the ambient light environment from my location is such that I don't think I'm ever fully dark-adapted, so instead I ballparked a value of 5 mm under typical conditions. I assumed further that the throughput of my optical system is about 75%, and I used Crumey's estimates of typical values of the field factors except for F (no subscript). For that, I took the number derived from the previous experiment (3.5) described above.
Clear nights at my site under normal aerosol-loading conditions in the air (it's dusty in the desert!) reach a sky brightness of about 20.0 magnitudes per square arcsecond in the Sky Quality Meter passband, which is a very rough approximation of the astronomical V band. Let's say for sake of argument it's about 20. Crumey's model then predicts that my point-source limit in V should be around +12.8 to +13.0. How does that compare to what I actually see?
I thought about some different ways to test this, mostly involving selecting stars on charts that were just over or under this range of magnitudes and asking myself if I could see them. But that's sort of a needle-in-a-haystack proposition. Then I thought: what if I could look at a whole group of stars roughly around that brightness? There are plenty of such examples. They're called globular star clusters. I had, for years, recorded in my notes when I observed them visually whether or not I could sense these objects beginning to resolve into individual stars. Unresolved globular look like a blur or smudge of light. If my eyes could sense the individual stars in the cluster, then they must be above my point-source limit. (Granting that this presents a modification that Crumey's model doesn't take into account, since the "sky" right next to one of these stars isn't really at the surface brightness of the night sky. But let's see what happens anyway.)
The next question is: how bright are those stars?
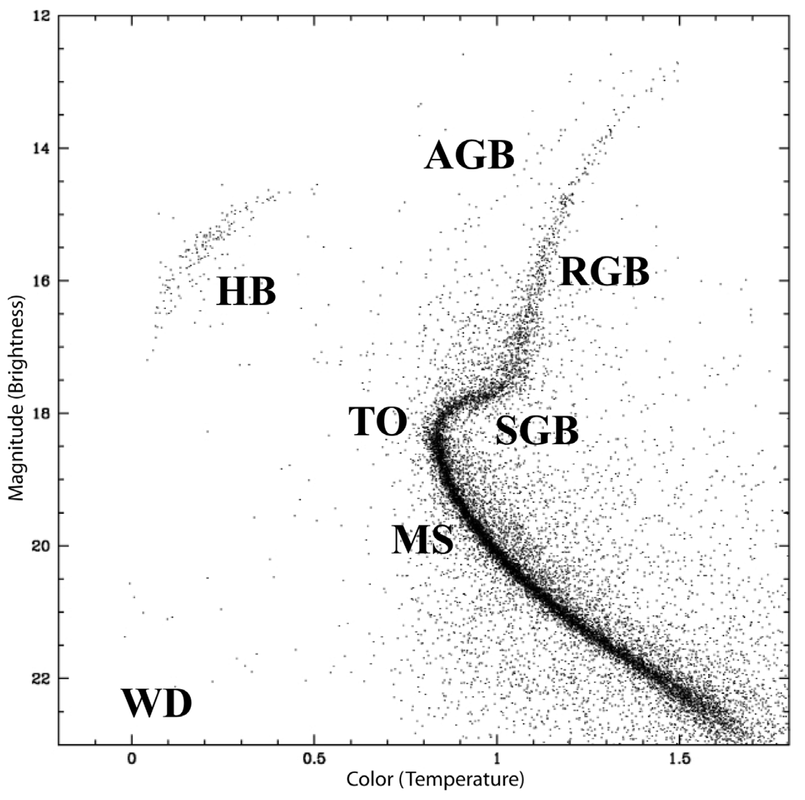
An indicator of this is the apparent brightness of the most luminous stars in any particular globular cluster, which is often a known quantity. My proxy for this is the so-called "TRGB", which in astronomical parlance stands for Tip of the Red Giant Branch. This refers to the luminous end of the population of red giant stars in a star cluster as revealed by plotting the brightnesses of stars in the cluster against their colors (being more red or more blue, on average). This kind of plot is commonly referred to as a "color-magnitude diagram" or a "Hertzsprung-Russell diagram". Here's an example for the globular star cluster Messier 12 from Figure 1.2 in Mix et al. (2006):
This formula suggests how the limiting magnitude would change with night sky brightness assuming all other variables are fixed, which is true for a given setup. All of my observations were made with a telescope for which D = 200 mm. The exit pupil is calculated as the the focal length of the eyepiece in millimeters divided by the focal ratio of the telescope (in my case, f/3.8). I typically observe with a 12.5 mm orthoscopic eyepiece that gives a magnification of 61× and a field of view of just about 0.5º. That means the exit pupil is about 3.3 mm. A lab measurement of the diameter of the dark-adapted pupil for people about my age is 6.15 mm (Bradley et al. 2011). However, the brightness of the ambient light environment from my location is such that I don't think I'm ever fully dark-adapted, so instead I ballparked a value of 5 mm under typical conditions. I assumed further that the throughput of my optical system is about 75%, and I used Crumey's estimates of typical values of the field factors except for F (no subscript). For that, I took the number derived from the previous experiment (3.5) described above.
Clear nights at my site under normal aerosol-loading conditions in the air (it's dusty in the desert!) reach a sky brightness of about 20.0 magnitudes per square arcsecond in the Sky Quality Meter passband, which is a very rough approximation of the astronomical V band. Let's say for sake of argument it's about 20. Crumey's model then predicts that my point-source limit in V should be around +12.8 to +13.0. How does that compare to what I actually see?
I thought about some different ways to test this, mostly involving selecting stars on charts that were just over or under this range of magnitudes and asking myself if I could see them. But that's sort of a needle-in-a-haystack proposition. Then I thought: what if I could look at a whole group of stars roughly around that brightness? There are plenty of such examples. They're called globular star clusters. I had, for years, recorded in my notes when I observed them visually whether or not I could sense these objects beginning to resolve into individual stars. Unresolved globular look like a blur or smudge of light. If my eyes could sense the individual stars in the cluster, then they must be above my point-source limit. (Granting that this presents a modification that Crumey's model doesn't take into account, since the "sky" right next to one of these stars isn't really at the surface brightness of the night sky. But let's see what happens anyway.)
The next question is: how bright are those stars?
An indicator of this is the apparent brightness of the most luminous stars in any particular globular cluster, which is often a known quantity. My proxy for this is the so-called "TRGB", which in astronomical parlance stands for Tip of the Red Giant Branch. This refers to the luminous end of the population of red giant stars in a star cluster as revealed by plotting the brightnesses of stars in the cluster against their colors (being more red or more blue, on average). This kind of plot is commonly referred to as a "color-magnitude diagram" or a "Hertzsprung-Russell diagram". Here's an example for the globular star cluster Messier 12 from Figure 1.2 in Mix et al. (2006):
Groups of different kinds of stars in the cluster are labeled with capital letters. The red giant stars are found in the "Red Giant Branch" (RGB). Since all the stars in the cluster are at about the same distance from Earth, their position in the vertical direction on the plot corresponds to their luminosity (absolute brightness). The spray of points arching toward the upper right that represents the RGB fizzles out at around magnitude 12.5 (the "tip" of the RGB). So the brightest stars one might observe in this globular cluster have an apparent magnitude in that neighborhood. All other stars in the cluster are less luminous than these giant stars, and so their apparent brightnesses are lower.
So one means of guessing the point-source limit of telescopic observations is to ask whether an observer is able to discern these individual stars. If yes, then the point source limit must be somewhere around the TRGB. If no, then the observer sees not individual stars but the sum of starlight of many thousands of stars, none of which is individually resolved. I dug into my records to see what I could find.
I recorded observations of 32 globular star clusters that included some remark on whether the clusters were (or were not) visually resolved into stars. All of these observations were for my current home observatory site and my current setup with the telescope and eyepiece combination described above. For each, in addition to whether I visually resolved it into stars, I also noted its Shapley–Sawyer Concentration Class (a measure of how centrally condensed the cluster is) and the V-band magnitude of its TRGB from sources in the astronomy literature. I classified the resolution of the clusters I observed into stars along three directions: definite detections ("Y"), definite non-detections ("N") and cases where I was either unsure or had a vague sense of resolution into stars ("liminal"). The following table of results is sorted first on whether the cluster was visually resolved, then on the magnitude of its TRGB from brightest to faintest.
So one means of guessing the point-source limit of telescopic observations is to ask whether an observer is able to discern these individual stars. If yes, then the point source limit must be somewhere around the TRGB. If no, then the observer sees not individual stars but the sum of starlight of many thousands of stars, none of which is individually resolved. I dug into my records to see what I could find.
I recorded observations of 32 globular star clusters that included some remark on whether the clusters were (or were not) visually resolved into stars. All of these observations were for my current home observatory site and my current setup with the telescope and eyepiece combination described above. For each, in addition to whether I visually resolved it into stars, I also noted its Shapley–Sawyer Concentration Class (a measure of how centrally condensed the cluster is) and the V-band magnitude of its TRGB from sources in the astronomy literature. I classified the resolution of the clusters I observed into stars along three directions: definite detections ("Y"), definite non-detections ("N") and cases where I was either unsure or had a vague sense of resolution into stars ("liminal"). The following table of results is sorted first on whether the cluster was visually resolved, then on the magnitude of its TRGB from brightest to faintest.
Object |
Other designation |
Class |
Resolved? |
TRGB (mV) |
Source |
NGC 6656 |
Messier 22 |
VII |
Y |
+11.0 |
Richter, Hilker and Richtler (1999) |
NGC 5139 |
ω Centauri |
VIII |
Y |
+11.5 |
Rosenberg et al. (2000a) |
NGC 6121 |
Messier 4 |
IX |
Y |
+12.0 |
Kanatas et al. (1995) |
NGC 6333 |
Messier 9 |
VIII |
Y |
+12.0 |
Arellano Ferro et al. (2013) |
NGC 6205 |
Messier 13 |
V |
Y |
+12.1 |
Cohen et al. (1997) |
NGC 6218 |
Messier 12 |
IX |
Y |
+12.1 |
De Angeli et al. (2005) |
NGC 6838 |
Messier 71 |
X-XI |
Y |
+12.2 |
Hodder et al. (1992) |
NGC 5904 |
Messier 5 |
V |
Y |
+12.3 |
Piotto et al. (2002) |
NGC 5272 |
Messier 3 |
VI |
Y |
+12.5 |
Buonanno et al. (1994) |
NGC 6093 |
Messier 80 |
II |
Y |
+12.5 |
Alcaino et al. (1998) |
NGC 7078 |
Messier 15 |
IV |
Y |
+12.6 |
Piotto et al. (2002) |
NGC 6254 |
Messier 10 |
VII |
Y |
+13.0 |
Hurley et al. (1989) |
NGC 7089 |
Messier 2 |
II |
Y |
+13.0 |
Lee and Carney (1999) |
NGC 6779 |
Messier 56 |
X |
N |
+13.4 |
Rosenberg et al. (2000b) |
NGC 5897 |
GCL 33 |
XI |
N |
+13.5 |
Ferraro, Fusi Pecci and Buonanno (1992) |
NGC 5466 |
GCL 27 |
XII |
N |
+13.7 |
Buonanno et al. (1984) |
NGC 6934 |
GCL 117 |
VIII |
N |
+14.0 |
Piotto et al. (2002) |
NGC 6981 |
Messier 72 |
IX |
N |
+14.0 |
Piotto et al. (2002) |
NGC 5634 |
GCL 28 |
IV |
N |
+14.5 |
Bellazzini et al. (2002) |
NGC 6139 |
GCL 43 |
II |
N |
+14.5 |
Ortolani, Bica and Barbuy (1999) |
NGC 4147 |
GCL 18 |
VI |
N |
+14.7 |
Wang et al. (2000) |
NGC 6342 |
GCL 61 |
IV |
N |
+15.0 |
Piotto et al. (2002) |
NGC 6401 |
GCL 73 |
IX |
N |
+15.0 |
Piotto et al. (2002) |
NGC 6356 |
GCL 62 |
II |
N |
+15.2 |
Piotto et al. (2002) |
NGC 6229 |
GCL 47 |
IV |
N |
+15.4 |
Carney, Fullton and Trammell (1991) |
NGC 5694 |
GCL 29 |
IV |
N |
+16.0 |
Ortolani and Gratton (1990) |
NGC 6341 |
Messier 92 |
IV |
liminal |
+11.5 |
Paust, Chaboyer and Sarajedini (2007) |
NGC 7099 |
Messier 30 |
V |
liminal |
+12.7 |
Guhathakurta et al. (1998) |
NGC 4590 |
Messier 68 |
X |
liminal |
+12.8 |
Rosenberg et al. (2000a) |
NGC 6266 |
Messier 62 |
IV |
liminal |
+12.8 |
Rosenberg et al. (2000a) |
NGC 288 |
Melotte 3 |
X |
liminal |
+13.0 |
Alcaino, Liller and Alvarado (1997) |
NGC 6273 |
Messier 19 |
VIII |
liminal |
+13.5 |
Piotto et al. (1999) |
The observations fall roughly into this schema:
To me, that suggests that my telescopic point-source detection limit is somewhere around the range of magnitudes involved in those liminal cases of resolving globulars into their component stars. And indeed the numbers compare pretty well. Crumey's model predicts +12.8 to +13.0, and my liminal cases are +12.7 to +13.5. Not bad!
So I can take as a rule of thumb that under typical conditions at my site I should be able to visually detect point sources down to around magnitude +13. There are roughly 6.8 million stars in the night sky brighter than this, of which about 4.5 million are, in principle, observable from my site. (That's a lot of stars!)
What accounts for the differences? There are lots of unconstrained variables here, including the transparency of the night sky (which is somewhat related to its apparent brightness), the blurring effect of seeing, and aberrations in my optical system like coma. There's also some uncertainty in reading the color-magnitude diagrams in the papers listed above. Taken together, all that might well add up to a couple of tenths of a magnitude.
Why is this exercise useful? It helps me guess whether certain objects will or won't be visible — in particular, variable stars. If I know that the brightness of a particular variable is at or near my detection threshold, it bears on whether I will try to observe it. This helps improve observing efficiency given the light-polluted nature of my site. If the typical zenith brightness at my location were to decrease by half a magnitude per square arcsecond, I would pick up 0.2 magnitude in terms of seeing progressively fainter stars.
Knowing my point-source magnitude limit can also help with forecasting the visibility of transient objects like novae and supernovae. For example, here are my visual estimates of the brightness of supernova 2023ixf in the galaxy Messier 101, made from its first appearance in May 2023 through early July 2023.
- Clusters whose TRGB is at V magnitude +12.6 and brighter are likely to be resolved.
- Clusters whose TRGB is fainter than V magnitude +13.4 are unlikely to be resolved.
- Clusters whose TRGB is in the range of about +12.7 to +13.2 are likely to be only liminally resolved.
To me, that suggests that my telescopic point-source detection limit is somewhere around the range of magnitudes involved in those liminal cases of resolving globulars into their component stars. And indeed the numbers compare pretty well. Crumey's model predicts +12.8 to +13.0, and my liminal cases are +12.7 to +13.5. Not bad!
So I can take as a rule of thumb that under typical conditions at my site I should be able to visually detect point sources down to around magnitude +13. There are roughly 6.8 million stars in the night sky brighter than this, of which about 4.5 million are, in principle, observable from my site. (That's a lot of stars!)
What accounts for the differences? There are lots of unconstrained variables here, including the transparency of the night sky (which is somewhat related to its apparent brightness), the blurring effect of seeing, and aberrations in my optical system like coma. There's also some uncertainty in reading the color-magnitude diagrams in the papers listed above. Taken together, all that might well add up to a couple of tenths of a magnitude.
Why is this exercise useful? It helps me guess whether certain objects will or won't be visible — in particular, variable stars. If I know that the brightness of a particular variable is at or near my detection threshold, it bears on whether I will try to observe it. This helps improve observing efficiency given the light-polluted nature of my site. If the typical zenith brightness at my location were to decrease by half a magnitude per square arcsecond, I would pick up 0.2 magnitude in terms of seeing progressively fainter stars.
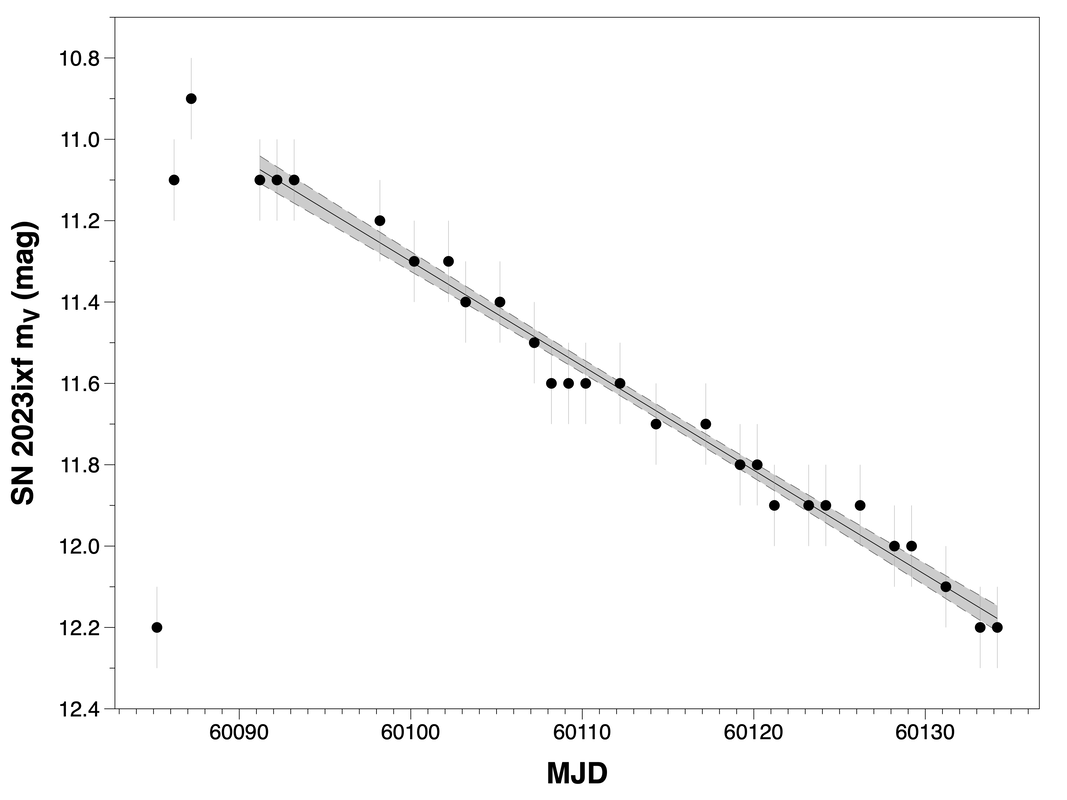
Knowing my point-source magnitude limit can also help with forecasting the visibility of transient objects like novae and supernovae. For example, here are my visual estimates of the brightness of supernova 2023ixf in the galaxy Messier 101, made from its first appearance in May 2023 through early July 2023.
This particular supernova is of a variety whose apparent brightness diminishes roughly linearly with time after its first appearance. My observations are well-fitted with a straight line whose slope is about 0.025 magnitudes per day; in other words, the supernova decreases in brightness by one magnitude (factor ~2.5) about every 39 days. The fit is shown with 95% confidence intervals in the shaded area. The r-squared value of this fit is 0.986, so the data describe a straight-line relationship pretty well.
For how long might this object be visible to me? Extrapolating the fit into the future suggests that will cross my point-source threshold on about 12 August 2023. After that, search as I might, it's unlikely that I will see SN 2023ixf again.
For how long might this object be visible to me? Extrapolating the fit into the future suggests that will cross my point-source threshold on about 12 August 2023. After that, search as I might, it's unlikely that I will see SN 2023ixf again.
References
Alcaino, G., Liller, W., & Alvarado, F. (1997). Multicolor NTT Photometry of the Anomalous Globular Cluster NGC 288. The Astronomical Journal, Vol. 114, p. 2626. https://doi.org/10.1086/118672
Alcaino, G., Liller, W., Alvarado, F., Kravtsov, V., Ipatov, A., Samus, N., & Smirnov, O. (1998). Multicolor CCD Photometry of the Poorly Studied Globular Cluster M80. The Astronomical Journal, Vol. 116, Issue 5, pp. 2415–2422. https://doi.org/10.1086/300587
Arellano Ferro, A., et al. (2013). A detailed census of variable stars in the globular cluster NGC 6333 (M9) from CCD differential photometry. Monthly Notices of the Royal Astronomical Society, Vol. 434, Issue 2, pp. 1220–1238. https://doi.org/10.1093/mnras/stt1080
Bellazzini, M., Ferraro, F. R., & Ibata, R. (2002). The Stellar Population of NGC 5634: A Globular Cluster in the Sagittarius dSph Stream? The Astronomical Journal, Vol. 124, Issue 2, pp. 915–923. https://doi.org/10.1086/341755
Blackwell, H. R. (1946). Contrast Thresholds of the Human Eye. Journal of the Optical Society of America, Vol. 36, Issue 11, p. 624. https://doi.org/10.1364/josa.36.000624
Bradley, J. C., Bentley, K. C., Mughal, A. I., Bodhireddy, H., & Brown, S. M. (2011). Dark-Adapted Pupil Diameter as a Function of Age Measured with the NeurOptics Pupillometer. Journal of Refractive Surgery, Vol. 27, Issue 3, pp. 202–207. https://doi.org/10.3928/1081597x-20100511-01
Buonanno, R., Buscema, G., Corsi, C. E., Iannicola, G., Fusi Pecci, F. (1984). Positions, magnitudes and colors for stars in the globular cluster NGC 5466. Astronomy and Astrophysics, Supplement Series, Vol. 56, p. 79-86. No doi.
Buonanno, R., Corsi, C. E., Buzzoni, A., Cacciari, C., Ferraro, F. R., Fusi Pecci, F. (1994). The stellar population of the globular cluster M 3. I. Photographic photometry of 10000 stars. Astronomy and Astrophysics, Vol. 290, pp.69–103. No doi.
Carney, B. W., Fullton, L. K., & Trammell, S. R. (1991). The distant globular cluster NGC 6229 and its relation to other outer halo clusters. The Astronomical Journal, Vol. 101, p. 1699. https://doi.org/10.1086/115799
Cohen, R. L., Guhathakurta, P., Yanny, B., Schneider, D. P., & Bahcall, J. N. (1997). Globular Cluster Photometry with the Hubble Space Telescope.VI.WF/PC-I Observations of the Stellar Populations in the Core of M13 (NGC 6205). The Astronomical Journal, Vol. 113, p. 669. https://doi.org/10.1086/118285
Crumey, A. (2014). Human contrast threshold and astronomical visibility. Monthly Notices of the Royal Astronomical Society, Vol. 442, Issue 3, pp. 2600–2619. https://doi.org/10.1093/mnras/stu992
De Angeli, F., Piotto, G., Cassisi, S., Busso, G., Recio-Blanco, A., Salaris, M., Aparicio, A., & Rosenberg, A. (2005). Galactic Globular Cluster Relative Ages. The Astronomical Journal, Vol. 130, Issue 1, pp. 116–125. https://doi.org/10.1086/430723
Ferraro, F. R., Fusi Pecci, F., & Buonanno, R. (1992). The Galactic globular cluster NGC 5897 and its population of blue stragglers. Monthly Notices of the Royal Astronomical Society, Vol. 256, Issue 3, pp. 376–390. https://doi.org/10.1093/mnras/256.3.376
Guhathakurta, P., Webster, Z. T., Yanny, B., Schneider, D. P., & Bahcall, J. N. (1998). Globular Cluster Photometry with the Hubble Space Telescope. VII. Color Gradients and Blue Stragglers in the Central Region of M30 from Wide Field Planetary Camera 2 Observations. The Astronomical Journal, Vol. 116, Issue 4, pp. 1757–1774. https://doi.org/10.1086/300566
Hodder, P. J. C., Nemec, J. M., Richer, H. B., & Fahlman, G. G. (1992). Deep CCD photometry and variable stars in the metal-rich globular cluster M71. The Astronomical Journal, Vol. 103, p. 460. https://doi.org/10.1086/116075
Hurley, D. J. C., Richer, H. B., & Fahlman, G. G. (1989). Deep CCD photometry in globular cluster. IX - M10. The Astronomical Journal, Vol. 98, p. 2124. https://doi.org/10.1086/115283
Kanatas, I., Griffiths, W. K., Dickens, R. J., & Penny, A. J. (1995). CCD photometry in the globular cluster M4. Monthly Notices of the Royal Astronomical Society, Vol. 272, Issue 2, pp. 265–290. https://doi.org/10.1093/mnras/272.2.265
Knoll, H. A., Tousey, R., & Hulburt, E. O. (1946). Visual Thresholds of Steady Point Sources of Light in Fields of Brightness from Dark to Daylight. Journal of the Optical Society of America, Vol. 36, Issue 8, p. 480. https://doi.org/10.1364/josa.36.000480
Lee, J.-W., & Carney, B. W. (1999). BV Photometry of RR Lyrae Variables in the Globular Cluster M2 (NGC 7089). The Astronomical Journal, Vol. 117, Issue 6, pp. 2868–2881. https://doi.org/10.1086/300883
Mix, L.J., et al. (Eds.) (2006). The Astrobiology Primer: An Outline of General Knowledge—Version 1, 2006. Astrobiology, Vol. 6, Issue 5, pp. 735–813. https://doi.org/10.1089/ast.2006.6.735
Ortolani, S., Bica, E., & Barbuy, B. (1999). Blue horizontal branch globular clusters towards the bulge: Terzan 9, NGC 6139 and NGC 6453. Astronomy and Astrophysics Supplement Series, Vol. 138, Issue 2, pp. 267–273. https://doi.org/10.1051/aas:1999275
Ortolani, S., & Gratton, R. (1990). Deep photometry of globular clusters. XII. The metal-poor clusters NGC 5694 and Terzan 8. Astronomy and Astrophysics Supplement Series, Vol. 82, p. 71-112. No doi.
Paust, N. E. Q., Chaboyer, B., & Sarajedini, A. (2007). BVI Photometry and the Luminosity Functions of the Globular Cluster M92. The Astronomical Journal, Vol. 133, Issue 6, pp. 2787–2798. https://doi.org/10.1086/513511
Piotto, G., King, I. R., Djorgovski, S. G., Sosin, C., Zoccali, M., Saviane, I., De Angeli, F., Riello, M., Recio Blanco, A., Rich, R. M., Meylan, G., & Renzini, A. (2002). HST color-magnitude diagrams of 74 galactic globular clusters in the HST F439W and F555W bands. Astronomy & Astrophysics, Vol. 391, Issue 3, pp. 945–965. https://doi.org/10.1051/0004-6361:20020820
Richter, P., Hilker, M., & Richtler, T. (1999). Stroemgren photometry of globular clusters: M55 & M22 (Version 1). arXiv. https://doi.org/10.48550/ARXIV.ASTRO-PH/9907200
Rosenberg, A., Piotto, G., Saviane, I., & Aparicio, A. (2000a). Photometric catalog of nearby globular clusters. Astronomy and Astrophysics Supplement Series, Vol. 144, Issue 1, pp. 5–38. https://doi.org/10.1051/aas:2000341
Rosenberg, A., Aparicio, A., Saviane, I., & Piotto, G. (2000b). Photometric catalog of nearby globular clusters. Astronomy and Astrophysics Supplement Series, Vol. 145, Issue 3, pp. 451–465. https://doi.org/10.1051/aas:2000356
Wang, J. J., Chen, L., Wu, Z. Y., Gupta, A. C., & Geffert, M. (2000). Kinematics and CMD of the globular cluster NGC 4147. Astronomy and Astrophysics Supplement Series, Vol. 142, Issue 3, pp. 373–387. https://doi.org/10.1051/aas:2000158
Alcaino, G., Liller, W., Alvarado, F., Kravtsov, V., Ipatov, A., Samus, N., & Smirnov, O. (1998). Multicolor CCD Photometry of the Poorly Studied Globular Cluster M80. The Astronomical Journal, Vol. 116, Issue 5, pp. 2415–2422. https://doi.org/10.1086/300587
Arellano Ferro, A., et al. (2013). A detailed census of variable stars in the globular cluster NGC 6333 (M9) from CCD differential photometry. Monthly Notices of the Royal Astronomical Society, Vol. 434, Issue 2, pp. 1220–1238. https://doi.org/10.1093/mnras/stt1080
Bellazzini, M., Ferraro, F. R., & Ibata, R. (2002). The Stellar Population of NGC 5634: A Globular Cluster in the Sagittarius dSph Stream? The Astronomical Journal, Vol. 124, Issue 2, pp. 915–923. https://doi.org/10.1086/341755
Blackwell, H. R. (1946). Contrast Thresholds of the Human Eye. Journal of the Optical Society of America, Vol. 36, Issue 11, p. 624. https://doi.org/10.1364/josa.36.000624
Bradley, J. C., Bentley, K. C., Mughal, A. I., Bodhireddy, H., & Brown, S. M. (2011). Dark-Adapted Pupil Diameter as a Function of Age Measured with the NeurOptics Pupillometer. Journal of Refractive Surgery, Vol. 27, Issue 3, pp. 202–207. https://doi.org/10.3928/1081597x-20100511-01
Buonanno, R., Buscema, G., Corsi, C. E., Iannicola, G., Fusi Pecci, F. (1984). Positions, magnitudes and colors for stars in the globular cluster NGC 5466. Astronomy and Astrophysics, Supplement Series, Vol. 56, p. 79-86. No doi.
Buonanno, R., Corsi, C. E., Buzzoni, A., Cacciari, C., Ferraro, F. R., Fusi Pecci, F. (1994). The stellar population of the globular cluster M 3. I. Photographic photometry of 10000 stars. Astronomy and Astrophysics, Vol. 290, pp.69–103. No doi.
Carney, B. W., Fullton, L. K., & Trammell, S. R. (1991). The distant globular cluster NGC 6229 and its relation to other outer halo clusters. The Astronomical Journal, Vol. 101, p. 1699. https://doi.org/10.1086/115799
Cohen, R. L., Guhathakurta, P., Yanny, B., Schneider, D. P., & Bahcall, J. N. (1997). Globular Cluster Photometry with the Hubble Space Telescope.VI.WF/PC-I Observations of the Stellar Populations in the Core of M13 (NGC 6205). The Astronomical Journal, Vol. 113, p. 669. https://doi.org/10.1086/118285
Crumey, A. (2014). Human contrast threshold and astronomical visibility. Monthly Notices of the Royal Astronomical Society, Vol. 442, Issue 3, pp. 2600–2619. https://doi.org/10.1093/mnras/stu992
De Angeli, F., Piotto, G., Cassisi, S., Busso, G., Recio-Blanco, A., Salaris, M., Aparicio, A., & Rosenberg, A. (2005). Galactic Globular Cluster Relative Ages. The Astronomical Journal, Vol. 130, Issue 1, pp. 116–125. https://doi.org/10.1086/430723
Ferraro, F. R., Fusi Pecci, F., & Buonanno, R. (1992). The Galactic globular cluster NGC 5897 and its population of blue stragglers. Monthly Notices of the Royal Astronomical Society, Vol. 256, Issue 3, pp. 376–390. https://doi.org/10.1093/mnras/256.3.376
Guhathakurta, P., Webster, Z. T., Yanny, B., Schneider, D. P., & Bahcall, J. N. (1998). Globular Cluster Photometry with the Hubble Space Telescope. VII. Color Gradients and Blue Stragglers in the Central Region of M30 from Wide Field Planetary Camera 2 Observations. The Astronomical Journal, Vol. 116, Issue 4, pp. 1757–1774. https://doi.org/10.1086/300566
Hodder, P. J. C., Nemec, J. M., Richer, H. B., & Fahlman, G. G. (1992). Deep CCD photometry and variable stars in the metal-rich globular cluster M71. The Astronomical Journal, Vol. 103, p. 460. https://doi.org/10.1086/116075
Hurley, D. J. C., Richer, H. B., & Fahlman, G. G. (1989). Deep CCD photometry in globular cluster. IX - M10. The Astronomical Journal, Vol. 98, p. 2124. https://doi.org/10.1086/115283
Kanatas, I., Griffiths, W. K., Dickens, R. J., & Penny, A. J. (1995). CCD photometry in the globular cluster M4. Monthly Notices of the Royal Astronomical Society, Vol. 272, Issue 2, pp. 265–290. https://doi.org/10.1093/mnras/272.2.265
Knoll, H. A., Tousey, R., & Hulburt, E. O. (1946). Visual Thresholds of Steady Point Sources of Light in Fields of Brightness from Dark to Daylight. Journal of the Optical Society of America, Vol. 36, Issue 8, p. 480. https://doi.org/10.1364/josa.36.000480
Lee, J.-W., & Carney, B. W. (1999). BV Photometry of RR Lyrae Variables in the Globular Cluster M2 (NGC 7089). The Astronomical Journal, Vol. 117, Issue 6, pp. 2868–2881. https://doi.org/10.1086/300883
Mix, L.J., et al. (Eds.) (2006). The Astrobiology Primer: An Outline of General Knowledge—Version 1, 2006. Astrobiology, Vol. 6, Issue 5, pp. 735–813. https://doi.org/10.1089/ast.2006.6.735
Ortolani, S., Bica, E., & Barbuy, B. (1999). Blue horizontal branch globular clusters towards the bulge: Terzan 9, NGC 6139 and NGC 6453. Astronomy and Astrophysics Supplement Series, Vol. 138, Issue 2, pp. 267–273. https://doi.org/10.1051/aas:1999275
Ortolani, S., & Gratton, R. (1990). Deep photometry of globular clusters. XII. The metal-poor clusters NGC 5694 and Terzan 8. Astronomy and Astrophysics Supplement Series, Vol. 82, p. 71-112. No doi.
Paust, N. E. Q., Chaboyer, B., & Sarajedini, A. (2007). BVI Photometry and the Luminosity Functions of the Globular Cluster M92. The Astronomical Journal, Vol. 133, Issue 6, pp. 2787–2798. https://doi.org/10.1086/513511
Piotto, G., King, I. R., Djorgovski, S. G., Sosin, C., Zoccali, M., Saviane, I., De Angeli, F., Riello, M., Recio Blanco, A., Rich, R. M., Meylan, G., & Renzini, A. (2002). HST color-magnitude diagrams of 74 galactic globular clusters in the HST F439W and F555W bands. Astronomy & Astrophysics, Vol. 391, Issue 3, pp. 945–965. https://doi.org/10.1051/0004-6361:20020820
Richter, P., Hilker, M., & Richtler, T. (1999). Stroemgren photometry of globular clusters: M55 & M22 (Version 1). arXiv. https://doi.org/10.48550/ARXIV.ASTRO-PH/9907200
Rosenberg, A., Piotto, G., Saviane, I., & Aparicio, A. (2000a). Photometric catalog of nearby globular clusters. Astronomy and Astrophysics Supplement Series, Vol. 144, Issue 1, pp. 5–38. https://doi.org/10.1051/aas:2000341
Rosenberg, A., Aparicio, A., Saviane, I., & Piotto, G. (2000b). Photometric catalog of nearby globular clusters. Astronomy and Astrophysics Supplement Series, Vol. 145, Issue 3, pp. 451–465. https://doi.org/10.1051/aas:2000356
Wang, J. J., Chen, L., Wu, Z. Y., Gupta, A. C., & Geffert, M. (2000). Kinematics and CMD of the globular cluster NGC 4147. Astronomy and Astrophysics Supplement Series, Vol. 142, Issue 3, pp. 373–387. https://doi.org/10.1051/aas:2000158